导入 numpy
约定俗成的以 np为numpy简称的导入方式
import numpy as np
numpy.array
创建一个数组
- 参数:
- object:类数组
- dtype:数据类型(data-type),默认为 None
- copy:是否拷贝,默认为 True
- order:内存布局(’K’,’A’,’C’,’F’),默认为 ‘K’
- subok:传递子类还是基类,默认为 False,即传递基类
- ndmin:最小维度,默认为 0
- 返回值:
一些简单的🌰
- 创建一个简单一维数组
- 创建一个简单二维数组
1
2
3
4
|
np.array([[1, 2],
[3, 4]])
|
- 创建一个最小维度为 2 的数组
1
2
|
np.array([1,2,3], ndmin=2)
|
- 使用矩阵创建数组
1
2
3
|
np.array(np.mat('1 2; 3 4'))
|
- 使用 array 返回子类
1
2
3
|
np.array(np.mat('1 2; 3 4'), subok=True)
|
ndarray
的一些常用属性
| 属性 |
解释 |
| ndim |
秩,即维度的数量 |
| shape |
数组的形状,即数组的维度 |
| size |
数组元素的总个数 |
| dtype |
其内元素类型 |
| itemsize |
每个元素的大小 |
| T |
转置 |
| flat |
数组的一维迭代器 |
ndarray
的一些常用方法
| 方法 |
解释 |
| astype() |
将类型转化为指定类型 |
| ravel() |
将数组展开成一维数组 |
| sum() |
数组元素求和 |
| all() |
是不是都为 True |
| any() |
是不是存在 True |
| argmax() |
最大值的索引 |
| max() |
最大值 |
| argmin() |
最小值的索引 |
| min() |
最小值 |
| argsort() |
排序的索引 |
| sort() |
排序 |
| dot() |
矩阵相乘 |
| fill() |
填充数据 |
| mean() |
平均值 |
| reshape() |
更改形状 |
| std() |
标准差 |
| var() |
方差 |
| nonzero() |
获取非零元素的索引 |
| put() |
用给定的值替换数组的指定元素 |
| transpose() |
转置,等同于 T |
| flatten() |
返回一份拷贝数组 |
| ptp() |
最大值与最小值的差 |
| average() |
加权平均值 |
数组的运算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
np.eye(2) + np.eye(2)
np.eye(2) - np.eye(2)
np.eye(2) * np.eye(2)
np.eye(2) / np.eye(2)
np.eye(2) @ np.eye(2)
np.eye(2) ** 2
np.eye(2) % 10
a = np.eye(2)
a.sum()
a.mean()
a.average()
a.max()
a.min()
np.median(a)
a.ptp()
a.var()
a.std()
np.sin(a)
np.cos(a)
np.tan(a)
np.floor(a)
np.ceil(a)
|
numpy.arange
返回给定间隔内均匀间隔的数组
-
参数
- start:开始值,默认为 0
- stop:结束值
- step:步长,默认为 1
- dtype:数据类型,默认为 None
-
返回值
一些简单的🌰
- 创建 0-2 的数组
- 创建一个 2-7 的数组
numpy.linspace
Return evenly spaced numbers over a specified interval.
返回指定间隔内的等间隔数字
- 参数
- start:开始值
- stop:结束值
- num:数量,默认为 50
- endpoint:是否包含stop 这个数字,默认为 True
- retstep:是否返回间隔数字之间的间隔,默认 False
- dtype:数据类型,默认为 None
- axis:按哪个轴获取。默认为 0
- 返回值:
- samples:ndarray
- step:步长,只有当 retstep 为True 时才有该值。
一些简单的🌰
- 创建一个 2.0 到 3.0 之间的 5 个等间距数字数组
1
2
|
np.linspace(2.0, 3.0, num=5)
|
- 上面的例子中,创建不包含结束值的数组
1
2
|
np.linspace(2.0, 3.0, num=5, endpoint=False)
|
- 第一个例子,返回步长
1
2
|
np.linspace(2.0, 3.0, num=5, retstep=True)
|
numpy.ones, numpy.zeros,
numpy.empty
ones:按照形状创建一个元素全为 1 的数组
zeros:按照形状创建一个元素全为 0 的数组
empty:按照形状创建一个元素全部无意义的数组
- 参数:
- shape:形状
- dtype:数据类型,默认为 None
- order:内存布局(’C’, ‘F’),默认为 C
- 返回值
一些简单的🌰
- 创建一个形状为 2 的数组
1
2
3
4
5
6
|
np.ones(2)
np.zeros(2)
np.empty(2)
|
- 创建一个形状为 (2, 2) 数组
1
2
3
4
5
6
7
8
9
|
np.ones((2, 2))
np.zeros((2, 2))
np.empty((2, 2))
|
numpy.eye(任意对角线为 1 的数组)
Return a 2-D array with ones on the diagonal and zeros elsewhere.
返回一个二维数组,对角线为 1,其他都为 0
- 参数:
- N:行数
- M:列数,默认等于行
- k:对角线索引,默认为 0,即主对角线,正数往右上平移,负数往左下平移。
- dtype:数据类型
- order:内存布局 (’C’, ‘F’),默认为 C
- 返回值
- I:ndarray of shape (N, M)
一些简单的🌰
- 创建一个 2 行 2 列的主对角线为 1 的数组
- 创建一个3 行 3 列,第 k=1 条对角线为 1 的数组
numpy.identity(单位数组)
返回单位数组,即主对角线为 1
该方法等同于 numpy.eye(n, M=n, k=0)
- 参数:
- n:行列数
- dtype:数据类型,默认为 None
- 返回值:
- 创建一个 2 行 2 列的主对角线为 1 的数组
行向量与列向量
numpy 中一维数组的行向量和列向量没有什么区别
1
2
3
|
a = np.arange(3)
a
a.T
|
二维的行列向量才有差别
1
2
3
4
5
6
|
a = np.array([[1, 2, 3]])
a
a.T
|
一维行向量变成二维列向量
1
2
3
4
5
6
|
a = np.arange(3)
a
a.reshape(-1, 1)
|
使用特殊方法创建行列向量
- 创建行向量
- 创建列向量
数组的切片和索引
一维数组的切片和索引
| 问 |
答 |
问 |
答 |
| 索引1 |
a[1] |
取[2, 5) |
a[2:5] |
| 步长 2 |
a[::2] |
倒序 |
a[::-1] |
二维数组的切片和索引
1
|
a = np.arange(25).reshape(5, 5)
|
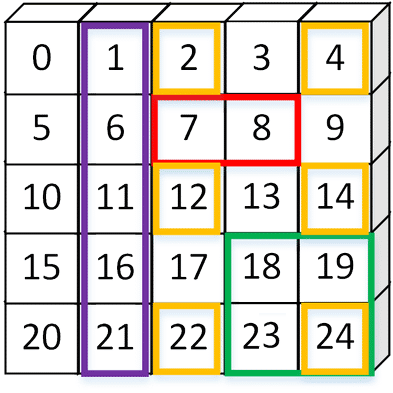
| 问 |
答 |
问 |
答 |
| 第一行 |
a[1] |
第一列 |
a[…,1]或a[:,1] |
| 取(1, 1)的元素 |
a[1, 1] |
紫色区域 |
a[…:1] |
| 红色区域 |
a[1, 2:4] |
绿色区域 |
a[-2:,-2:] |
| 黄色区域 |
a[::2, 2::2] |
黄色区域 |
a[::2, [2, 4]] |
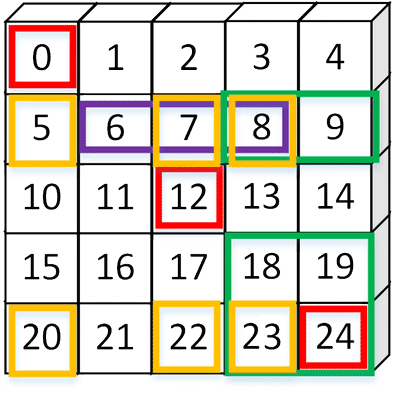
| 问 |
答 |
问 |
答 |
| 红色区域 |
a[[0, 2, 4],[0, 2, 4]] |
绿色区域 |
a[[1, 3 ,4], 3:] |
| 黄色区域 |
a[2::3, [0, 2, 3]] |
紫色区域 |
a[1,1:4] |
还有掩码切割的方式
- 黄色区域
1
2
|
mask = np.array([True, False, True, True, False])
a[1::3, mask]
|
- 紫色区域
1
2
|
mask = np.array([False, True, True, True, False])
a[1, mask]
|
数组拆分
1
|
a = np.arange(9).reshape(3, 3)
|
- 按行拆分
- 按列拆分
数组合并
1
2
|
a = np.arange(4).reshape(2, 2)
b = np.arange(4).reshape(2, 2)
|
- 竖直合并
- 水平合并
numpy的广播机制
以下内容来自菜鸟教程
广播的规则:
- 让所有输入数组都向其中形状最长的数组看齐,形状中不足的部分都通过在前面加 1 补齐。
- 输出数组的形状是输入数组形状的各个维度上的最大值。
- 如果输入数组的某个维度和输出数组的对应维度的长度相同或者其长度为 1 时,这个数组能够用来计算,否则出错。
- 当输入数组的某个维度的长度为 1 时,沿着此维度运算时都用此维度上的第一组值。
简单理解:对两个数组,分别比较他们的每一个维度(若其中一个数组没有当前维度则忽略),满足:
- 数组拥有相同形状。
- 当前维度的值相等。
- 当前维度的值有一个是 1。
若条件不满足,抛出 “ValueError: frames are not aligned” 异常。

